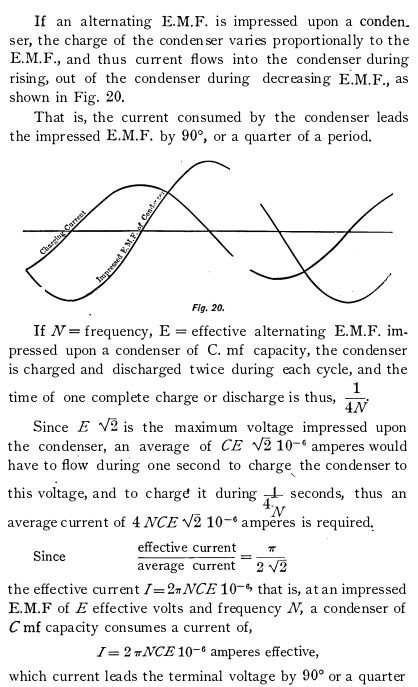
PART I.
GENERAL THEORY.
1. MAGNETISM AND ELECTRIC CURRENT.
A magnet pole attracting (or repelling) another magnet pole of equal strength at unit distance with unit force is called a unit magnet pole.
The space surrounding a magnet pole is called a magnetic field of force, or magnetic field.
The magnetic field at unit distance from a unit magnet pole is called a unit magnetic field, and is represented by one line of magnetic force (or shortly “one line”) per square centimeter. From a unit magnet pole, a total of [math] 4\pi [/math] lines of magnetic force issue.
The total number of lines of force issuing from a magnet pole is called its magnetic flux.
The magnetic flux [math] \Phi [/math] of a magnet pole of strength [math] m [/math] is given by:
[math] \Phi = 4 \pi m. [/math]
At a distance [math] R [/math] from a magnet pole of strength [math] m [/math], and therefore of flux [math] \Phi = 4 \pi m [/math], the magnetic field has the intensity:
[math] H = \frac{4\pi m}{4\pi R^2} = \frac{m}{R^2}, [/math]
since the [math] \Phi [/math] lines issuing from the pole distribute over the area of a sphere of radius [math] R [/math], that is, the area [math] 4\pi R^2 [/math].

In historical physics and engineering literature, especially texts grounded in the CGS electrostatic (ESU) system, one often encounters unit conversions involving seemingly peculiar numerical factors. A notable example is the constant [math]1.11 \times 10^{-6}[/math], which appears in equations converting CGS-based capacitance formulas into practical SI-based expressions, particularly when computing capacitance per unit length in coaxial or parallel-wire geometries.
To understand this factor, we begin with the fundamental conversion between capacitance units:
From classical sources:
- [math]1 \ \text{statfarad} = 1.111\ldots \times 10^{-12} \ \text{farads}[/math]
This is derived from the identity:
[math]
1 \ \text{statfarad} = \frac{1}{9 \times 10^{11}} \ \text{farads} = 1.111\ldots \times 10^{-12} \ \text{F}
[/math]
Converting farads into millifarads (noting that [math]1 \ \text{F} = 1000 \ \text{mf}[/math]):
[math]
1.111\ldots \times 10^{-12} \ \text{F} = 1.111\ldots \times 10^{-9} \ \text{mf}
[/math]
However, in several historical references, including early electromagnetic texts, the coefficient used in the capacitance per unit length formula is not [math]10^{-9}[/math], but rather:
[math]
C = 1.11 \times 10^{-6} \cdot \frac{l}{\log_e \left( \frac{2D}{d} \right)} \ \text{mf}
[/math]
At first glance, this appears inconsistent. The key lies in understanding the role and meaning of the coefficient [math]1.11 \times 10^{-6}[/math]. This constant is not merely a conversion from statfarads to farads; it encapsulates multiple layers of transformation:
- Conversion from statfarads per centimeter (CGS-ESU) to millifarads per meter (SI)
Since geometrical parameters like [math]l[/math], [math]d[/math], and [math]D[/math] are expressed in centimeters in the CGS system, while practical capacitance values are often required in SI-derived units (millifarads), the conversion must also account for a change in length scale (centimeters to meters). - Incorporation of the electrostatic constant [math]4\pi \varepsilon_0[/math]
SI expressions for capacitance include the vacuum permittivity constant, while ESU units embed it in the definition of the unit itself. Transitioning between systems involves absorbing this factor numerically. - Unit transformation to practical quantities
Engineers and physicists commonly express small capacitance values in millifarads for ease of calculation and readability. The factor [math]1.11 \times 10^{-6}[/math] is scaled accordingly.
In sum, the constant:
[math]
1.11 \times 10^{-6}
[/math]
functions as a compact numerical bridge between CGS electrostatic capacitance per centimeter and SI millifarads per meter, while inherently incorporating:
- The statfarad-to-farad conversion
- The centimeter-to-meter length scaling
- The absorption of physical constants specific to each system
- A rescaling to practical engineering units
It is best interpreted as the number of millifarads per centimeter per ESU unit of capacitance, appropriately scaled and normalized to fit into modern electrostatics expressions involving logarithmic geometry factors.
