CHAPTER IV.
THE LUMINIFEROUS MEDIUM, FROM BRADLEY TO FRESNEL.
Although Newton, as we have seen, refrained from committing himself to any doctrine regarding the ultimate nature of light, the writers of the next generation interpreted his criticism of the wave-theory as equivalent to an acceptance of the corpuscular hypothesis. As it happened, the chief optical discovery of this period tended to support the latter theory, by which it was first and most readily explained.
In 1728, James Bradley (b. 1692, d. 1762), at that time Savilian Professor of Astronomy at Oxford, sent to the Astronomer Royal (Halley) an Account of a New Discovered Motion of the Fix’d Stars. In observing the star γ in the head of the Dragon, he had found that during the winter of 1725–6, the transit across the meridian was continually more southerly, while during the following summer, its original position was restored by a motion northwards. Such an effect could not be explained as a result of parallax; and eventually, Bradley guessed it to be due to the gradual propagation of light.
Thus, let CACACA denote a ray of light, falling on the line BABABA; and suppose that the eye of the observer is travelling along BABABA with a velocity which is to the velocity of light as BABABA is to CACACA. Then the corpuscle of light, by which the object is discernible to the eye at AAA, would have been at CCC when the eye was at BBB. The tube of a telescope must therefore be pointed in the direction BCBCBC in order to receive the rays from an object whose light is really propagated in the direction CACACA. The angle BCABCABCA measures the difference between the real and apparent positions of the object; and it is evident from the figure that the sine of this angle is to the sine of the visible inclination of the object to the line in which the eye is moving, as the velocity of the eye is to the velocity of light.
Observations such as Bradley’s will therefore enable us to deduce the ratio of the mean orbital velocity of the earth to the velocity of light, or, as it is called, the constant of aberration; from its value, Bradley calculated that light is propagated from the sun to the earth in 8 minutes 12 seconds, which, as he remarked, “is as it were a Mean betwixt what had at different times been determined from the eclipses of Jupiter’s satellites.”
With the exception of Bradley’s discovery, which was primarily astronomical rather than optical, the eighteenth century was decidedly barren as regards both the experimental and the theoretical investigation of light, in curious contrast to the brilliance of its record in respect of electrical researches. But some attention must be given to a suggestive study of the aether, for which the younger John Bernoulli (b. 1710, d. 1790) was in 1736 awarded the prize of the French Academy.
The elder John Bernoulli (b. 1667, d. 1748) had made an attempt in 1701 to connect the law of refraction with the mechanical principle of the composition of forces. If two opposed forces, whose ratio is [math]\mu[/math], maintain in equilibrium a particle which is free to move only in a given plane, it follows from the triangle of forces that the directions of the forces must obey the relation
[math]\sin i = \mu \sin r[/math]
where [math]i[/math] and [math]r[/math] denote the angles made by these directions with the normals to the plane. This is the same equation that expresses the law of refraction, and the elder Bernoulli conjectured that a theory of light might be based on it. However, he gave no satisfactory physical reason for the existence of forces along the incident and refracted rays. His son now proceeded to remove this defect.
All space, according to the younger Bernoulli, is permeated by a fluid aether containing an immense number of excessively small whirlpools. The elasticity which the aether appears to possess, and in virtue of which it is able to transmit vibrations, is really due to the presence of these whirlpools; for, owing to centrifugal force, each whirlpool is continually striving to dilate and so presses against the neighbouring whirlpools. It will be seen that Bernoulli is a thorough Cartesian in spirit; not only does he reject action at a distance, but he insists that even the elasticity of his aether shall be explicable in terms of matter and motion.
This aggregate of small vortices, or fine-grained turbulent motion, as it came to be called a century and a half later, is interspersed with solid corpuscles, whose dimensions are small compared with their distances apart. These are pushed about by the whirlpools whenever the aether is disturbed, but never travel far from their original positions.
A source of light communicates to its surroundings a disturbance which condenses the nearest whirlpools; these, by their condensation, displace the contiguous corpuscles from their equilibrium positions; and these, in turn, produce condensations in the whirlpools next beyond them, so that vibrations are propagated in every direction from the luminous point. It is curious that Bernoulli speaks of these vibrations as longitudinal, and actually contrasts them with those of a stretched cord, which, “when it is slightly displaced from its rectilinear form, and then let go, performs transverse vibrations in a direction at right angles to the direction of the cord.”
When it is remembered that the objection to longitudinal vibrations, on the score of polarization, had already been clearly stated by Newton, and that Bernoulli’s aether closely resembles that which Maxwell invented in 1861–2 for the express purpose of securing transversality of vibration, one feels that perhaps no man ever so narrowly missed a great discovery.
Bernoulli explained refraction by combining these ideas with those of his father. Within the pores of ponderable bodies, the whirlpools are compressed, so the centrifugal force must vary in intensity from one medium to another. Thus, a corpuscle situated at the interface between two media is acted upon by a greater elastic force from one medium than from the other; and by applying the triangle of forces to find the conditions of its equilibrium, the law of Snell and Descartes may be obtained.
Not long after this, the echoes of the old controversy between Descartes and Fermat about the law of refraction were awakened by Pierre Louis Moreau de Maupertuis (b. 1698, d. 1759).
It will be remembered that, according to Descartes, the velocity of light is greatest in dense media, while according to Fermat, the propagation is swiftest in free aether. The arguments of the corpuscular theory convinced Maupertuis that, on this particular point, Descartes was in the right; but nevertheless, he wished to retain for science the beautiful method by which Fermat had derived his result.
This he now proposed to do by modifying Fermat’s principle so as to make it agree with the corpuscular theory. Instead of assuming that light follows the quickest path, he supposed that “the path described is that by which the quantity of action is the least”; and this action he defined to be proportional to the sum of the spaces described, each multiplied by the velocity with which it is traversed. Thus, instead of Fermat’s expression
[math]\int dt \quad \text{or} \quad \int \frac{ds}{v}[/math]
Accepting Newton’s doctrine that colour depends on wavelength, Euler in this memoir supposed the frequency to be greatest for red light and least for violet; but a few years later, he adopted the opposite opinion.
The chief novelty of Euler’s writings on light is his explanation of the manner in which material bodies appear coloured when viewed by white light, and, in particular, of the way in which the colours of thin plates are produced. He denied that such colours are due to a more copious reflection of light of certain particular periods and supposed that they represent vibrations generated within the body itself under the stimulus of the incident light. A coloured surface, according to this hypothesis, contains large numbers of elastic molecules, which, when agitated, emit light of a period depending only on their own structure. The colours of thin plates Euler explained in the same way; the elastic response and free period of the plate at any place would, he conceived, depend on its thickness at that place, and in this way, the dependence of the colour on the thickness was accounted for, the phenomena as a whole being analogous to well-known effects observed in experiments on sound.
An attempt to improve the corpuscular theory in another direction was made in 1752 by the Marquis de Courtivron, and independently in the following year by T. Melvill. These writers suggested, as an explanation of the different refrangibility of different colours, that “the differently coloured rays are projected with different velocities from the luminous body: the red with the greatest, violet with the least, and the intermediate colours with intermediate degrees of velocity.”
On this supposition, as its authors pointed out, the amount of aberration would be different for every different colour, and the satellites of Jupiter would change colour, from white through green to violet, through an interval of more than half a minute before their immersion into the planet’s shadow; while at emersion, the contrary succession of colours should be observed, beginning with red and ending in white. The testimony of practical astronomers was soon given that such appearances are not observed, and the hypothesis was accordingly abandoned.
The fortunes of the wave-theory began to brighten at the end of the century when a new champion arose. Thomas Young, born at Milverton in Somersetshire in 1773, and trained to the practice of medicine, began to write on optical theory in 1799. In his first paper, he remarked that, according to the corpuscular theory, the velocity of emission of a corpuscle must be the same in all cases, whether the projecting force be that of the feeble spark produced by the friction of two pebbles, or the intense heat of the sun itself—a thing almost incredible.
This difficulty does not exist in the undulatory theory since all disturbances are known to be transmitted through an elastic fluid with the same velocity. The reluctance which some philosophers felt to filling all space with an elastic fluid he met with an argument that strangely foreshadows the electric theory of light:
“That a medium resembling in many properties that which has been denominated ether does really exist is undeniably proved by the phenomena of electricity. The rapid transmission of the electrical shock shows that the electric medium is possessed of an elasticity as great as is necessary to be supposed for the propagation of light. Whether the electric ether is to be considered the same with the luminous ether, if such a fluid exists, may perhaps at some future time be discovered by experiment: hitherto I have not been able to observe that the refractive power of a fluid undergoes any change by electricity.”
Young then proceeds to show the superior power of the wave-theory to explain reflection and refraction. In the corpuscular theory, it is difficult to see why part of the light should be reflected and another part of the same beam refracted; but in the undulatory theory, there is no such trouble, as is shown by analogy with the partial reflection of sound from a cloud or a denser stratum of air:
“Nothing more is necessary than to suppose all refracting media to retain, by their attraction, a greater or less quantity of the luminous ether, so as to make its density greater than that which it possesses in a vacuum, without increasing its elasticity.”
This is precisely the hypothesis later adopted by Fresnel and Green.
In 1801, Young made a discovery of the first magnitude when attempting to explain Newton’s rings on the principles of the wave-theory. Rejecting Euler’s hypothesis of induced vibrations, he assumed that the colours observed all exist in the incident light and showed that they could be derived from it by a process which was now, for the first time, recognized in optical science.
The idea of this process was not altogether new, for it had been used by Newton in his theory of the tides. “It may happen,” he wrote,
“that the tide may be propagated from the ocean through different channels towards the same port, and may pass in less time through some channels than through others, in which case the same generating tide, being thus divided into two or more succeeding one another, may produce by composition new types of tide.”
Newton applied this principle to explain the anomalous tides at Batsha in Tonkin, which had previously been described by Halley.
Young’s own illustration of the principle is evidently suggested by Newton’s.
“Suppose,” he says, “a number of equal waves of water to move upon the surface of a stagnant lake, with a certain constant velocity, and to enter a narrow channel leading out of the lake; suppose then another similar cause to have excited another equal series of waves, which arrive at the same channel, with the same velocity, and at the same time with the first. Neither series of waves will destroy the other, but their effects will be combined; if they enter the channel in such a manner that the elevations of one series coincide with those of the other, they must together produce a series of greater joint elevations; but if the elevations of one series are so situated as to correspond to the depressions of the other, they must exactly fill up those depressions, and the surface of the water must remain smooth. Now I maintain that similar effects take place whenever two portions of light are thus mixed; and this I call the general law of the interference of light.”
Thus,
“whenever two portions of the same light arrive at the eye by different routes, either exactly or very nearly in the same direction, the light becomes most intense when the difference of the routes is any multiple of a certain length, and least intense in the intermediate state of the interfering portions; and this length is different for light of different colours.”
Young’s explanation of the colours of thin plates, as seen by reflection, was then that the incident light gives rise to two beams which reach the eye: one of these beams has been reflected at the first surface of the plate, and the other at the second surface; and these two beams produce the colours by their interference.
One difficulty encountered in reconciling this theory with observation arose from the fact that the central spot in Newton’s rings (where the thickness of the thin film of air is zero) is black and not white, as it would be if the interfering beams were similar to each other in all respects.
To account for this, Young showed, by analogy with the impact of elastic bodies, that when light is reflected at the surface of a denser medium, its phase is retarded by half an undulation, so that the interfering beams at the centre of Newton’s rings destroy each other. The correctness of this assumption he verified by substituting essence of sassafras (whose refractive index is intermediate between those of crown and flint glass) for air in the space between the lenses; as he anticipated, the centre of the ring-system was now white.
Newton had long before observed that the rings are smaller when the medium producing them is optically more dense. Interpreted by Young’s theory, this definitely proved that the wavelength of light is shorter in dense media, and therefore that its velocity is less.
The publication of Young’s papers occasioned a fierce attack on him in the Edinburgh Review, from the pen of Henry Brougham, afterwards Lord Chancellor of England. Young replied in a pamphlet, of which it is said that only a single copy was sold; and there can be no doubt that Brougham, for the time being, achieved his object of discrediting the wave-theory.
Young now turned his attention to the fringes of shadows. In the corpuscular explanation of these, it was supposed that the attractive forces which operate in refraction extend their influence to some distance from the surfaces of bodies and inflect such rays as pass close by. If this were the case, the amount of inflexion should obviously depend on the strength of the attractive forces, and consequently on the refractive indices of the bodies—a proposition that had been refuted by the experiments of s’Gravesande. The cause of diffraction effects was thus wholly unknown, until Young, in the Bakerian Lecture for 1803, showed that the principle of interference is concerned in their formation.
For when a hair is placed in the cone of rays diverging from a luminous point, the internal fringes (i.e. those within the geometrical shadow) disappear when the light passing on one side of the hair is intercepted. His conjecture as to the origin of the interfering rays was not so fortunate; for he attributed the fringes outside the geometrical shadow to interference between the direct rays and rays reflected at the diffracting edge and supposed the internal fringes of the shadow of a narrow object to be due to the interference of rays inflected by the two edges of the object.
The success of so many developments of the wave-theory led Young to inquire more closely into its capacity for solving the chief outstanding problem of optics—that of the behaviour of light in crystals. The beautiful construction for the extraordinary ray given by Huygens had lain neglected for a century, and the degree of accuracy with which it represented the observations was unknown. At Young’s suggestion, Wollaston investigated the matter experimentally and showed that the agreement between his own measurements and Huygens’ rule was remarkably close.
“I think,” he wrote, “the result must be admitted to be highly favourable to the Huygenian theory; and, although the existence of two refractions at the same time, in the same substance, be not well accounted for, and still less their interchange with each other, when a ray of light is made to pass through a second piece of spar situated transversely to the first, yet the oblique refraction, when considered alone, seems nearly as well explained as any other optical phenomenon.”
Meanwhile, the advocates of the corpuscular theory were not idle; and in the next few years, a succession of discoveries on their part, both theoretical and experimental, seemed likely to imperil the good position to which Young had advanced the rival hypothesis.
The first of these was a dynamical explanation of the refraction of the extraordinary ray in crystals, which was published in 1808 by Laplace. His method is an extension of that by which Maupertuis had accounted for the refraction of the ordinary ray, and which, since Maupertuis’ day, had been so developed that it was now possible to apply it to problems of all degrees of complexity.
Laplace assumes that the crystalline medium acts on the light-corpuscles of the extraordinary ray so as to modify their velocity, in a ratio that depends on the inclination of the extraordinary ray to the axis of the crystal: so that, in fact, the difference of the squares of the velocities of the ordinary and extraordinary rays is proportional to the square of the sine of the angle [math]{\theta}[/math] that the latter ray makes with the axis,
[math]{ v_e^2 – v_o^2 \propto \sin^2 \theta }[/math]
where [math]{ v_o }[/math] and [math]{ v_e }[/math] are the velocities of the ordinary and extraordinary rays, respectively.
The principle of least action then leads to a law of refraction identical with that found by Huygens’ construction with the spheroid, just as Maupertuis’ investigation led to a law of refraction for the ordinary ray identical with that found by Huygens’ construction with the sphere.
The law of refraction for the extraordinary ray may also be deduced from Fermat’s principle of least time, provided that the velocity is taken inversely proportional to that assumed in the principle of least action; and the velocity appropriate to Fermat’s principle agrees with that found by Huygens, being, in fact, proportional to the radius of the spheroid. These results are obvious extensions of those already obtained for ordinary refraction.
Laplace’s theory was promptly attacked by Young, who pointed out the improbability of such a system of forces as would be required to impress the requisite change of velocity on the light-corpuscles. If the aim of controversial matter is to convince the contemporary world, Young’s paper must be counted unsuccessful; but it permanently enriched science by proposing a dynamical foundation for double refraction on the principles of the wave-theory.
“A solution,” he says, “might be deduced upon the Huygenian principles, from the simplest possible supposition, that of a medium more easily compressible in one direction than in any direction perpendicular to it, as if it consisted of an infinite number of parallel plates connected by a substance somewhat less elastic. Such a structure of the elementary atoms of the crystal may be understood by comparing them to a block of wood or of mica. Mr. Chladni found that the mere obliquity of the fibres of a rod of Scotch fir reduced the velocity with which it transmitted sound in the proportion of 4 to 5. It is therefore obvious that a block of such wood must transmit every impulse in spheroidal—that is, oval—undulations; and it may also be demonstrated, as we shall show at the conclusion of this article, that the spheroid will be truly elliptical when the body consists either of plane and parallel strata, or of equidistant fibres, supposing both to be extremely thin, and to be connected by a less highly elastic substance; the spheroid being in the former case oblate and in the latter oblong.”
Young then proceeds to a formal proof that
“an impulse is propagated through every perpendicular section of a lamellar elastic substance in the form of an elliptic undulation.”
This must be regarded as the beginning of the dynamical theory of light in crystals. It was confirmed in a striking way not long afterwards by Brewster, who found that compression in one direction causes an isotropic transparent solid to become doubly refracting.
Meanwhile, in January 1808, the French Academy had proposed as the subject for the physical prize in 1810,
“To furnish a mathematical theory of double refraction, and to confirm it by experiment.”
Among those who resolved to compete was Etienne Louis Malus (b. 1775, d. 1812), a colonel of engineers who had seen service with Napoleon’s expedition to Egypt.
While conducting experiments towards the end of 1808 in a house in the Rue des Enfers in Paris, Malus happened to analyze with a rhomb of Iceland spar the light of the setting sun reflected from the window of the Luxembourg, and was surprised to notice that the two images were of very different intensities. Following up this observation, he found that light which had been reflected from glass acquires thereby a modification similar to that which Huygens had noticed in rays that have experienced double refraction, and which Newton had explained by supposing rays of light to have “sides.”
This discovery appeared so important that, without waiting for the prize competition, he communicated it to the Academy in December 1808 and published it in the following month.
“I have found,” he said, “that this singular disposition, which has hitherto been regarded as one of the peculiar effects of double refraction, can be completely impressed on the luminous molecules by all transparent solids and liquids.”
“For example, light reflected by the surface of water at an angle of [math]{ 52^\circ 45′ }[/math] has all the characteristics of one of the beams produced by the double refraction of Iceland spar, whose principal section is parallel to the plane which passes through the incident ray and the reflected ray. If we receive this reflected ray on any doubly-refracting crystal, whose principal section is parallel to the plane of reflection, it will not be divided into two beams as a ray of ordinary light would be, but will be refracted according to the ordinary law.”
After this, Malus found that light that has been refracted at the surface of any transparent substance likewise possesses, in some degree, this property, to which he gave the name polarization. The memoir which he finally submitted to the Academy, containing a rich store of experimental and analytical work on double refraction, obtained the prize in 1810. Its immediate effect regarding the rival theories of the ultimate nature of light was to encourage the adherents of the corpuscular doctrine, for it brought into greater prominence the phenomena of polarization, of which the wave-theorists, still misled by the analogy of light with sound, were unable to give any account.
The successful discoverer was elected to the Academy of Sciences and became a member of the celebrated club of Arcueil. However, his health, which had been undermined by the Egyptian campaign, now broke down completely, and he died at the age of thirty-six in the following year.
The polarization of a reflected ray is, in general, incomplete—i.e., the ray displays only imperfectly the properties of light that has been polarized by double refraction. However, for one particular angle of incidence, which depends on the reflecting body, the polarization of the reflected ray is complete. Malus measured with considerable accuracy the polarizing angles for glass and water and attempted to connect them with the other optical constants of these substances, the refractive indices, and dispersive powers, but without success.
The matter was afterwards taken up by David Brewster (b. 1781, d. 1868), who, in 1815, showed that there is complete polarization by reflection when the reflected and refracted rays satisfy the condition of being at right angles to each other.
Almost at the same time, Brewster made another discovery that profoundly affected the theory of double refraction. It had till then been believed that double refraction is always of the type occurring in Iceland spar, to which Huygens’ construction is applicable. Brewster now found this belief to be erroneous and showed that in a large class of crystals, there are two axes, instead of one, along which there is no double refraction. Such crystals are called biaxial, the simpler type to which Iceland spar belongs being called uniaxial.
At this time, the wave-theory was still encumbered with difficulties. Diffraction was not satisfactorily explained; for polarization, no explanation of any kind was forthcoming; the Huygenian construction appeared to require two different luminiferous media within doubly refracting bodies; and the universality of that construction had been impugned by Brewster’s discovery of biaxial crystals.
The upholders of the emission theory, emboldened by the success of Laplace’s theory of double refraction, thought the time ripe for their final triumph. As a step toward this, in March 1817, they proposed Diffraction as the subject of the Academy’s prize for 1818. Their expectation was disappointed; the successful memoir afforded the first of a series of reverses by which, in the short space of seven years, the corpuscular theory was completely overthrown.
The author was Augustin Fresnel (b. 1788, d. 1827), the son of an architect and himself a civil engineer in the Government service in Normandy. During the brief dominance of Napoleon after his escape from Elba in 1815, Fresnel fell into trouble for having enlisted in the small army that attempted to bar the exile’s return. During a period of enforced idleness following his arrest, he commenced to study diffraction.
In his earliest memoir, he propounded a theory similar to that of Young, which was flawed, like Young’s theory, by the assumption that the fringes depend on light reflected by the diffracting edge. Observing, however, that the blunt and sharp edges of a knife produce exactly the same fringes, he became dissatisfied with this attempt. On July 15th, 1816, he presented to the Academy a supplement to his paper, in which, for the first time, diffraction effects are referred to their true cause—namely, the mutual interference of the secondary waves emitted by those portions of the original wave-front that have not been obstructed by the diffracting screen.
Fresnel’s method of calculation utilized the principles of both Huygens and Young; he summed the effects due to different portions of the same primary wave-front, with due regard to the differences of phase engendered in propagation.
The sketch presented to the Academy in 1816 was, during the next two years, developed into an exhaustive memoir, which was submitted for the Academy’s prize.
It so happened that the earliest memoir, which had been presented to the Academy in the autumn of 1815, had been referred to a Commission of which the reporter was François Arago (b. 1786, d. 1853). Arago was so much impressed that he sought the friendship of the author, of whom he was later a strenuous champion.
A champion was indeed needed when the larger memoir was submitted; for Laplace, Poisson, and Biot, who constituted a majority of the Commission to which it was referred, were all zealous supporters of the corpuscular theory. During the examination, however, Fresnel was vindicated in a somewhat curious way.
He had calculated in the memoir the diffraction patterns of a straight edge, of a narrow opaque body bounded by parallel sides, and of a narrow opening bounded by parallel edges, and had shown that the results agreed excellently with his experimental measures. Poisson, when reading the manuscript, happened to notice that the analysis could be extended to other cases, and in particular that it would indicate the existence of a bright spot at the centre of the shadow of a circular screen.
He suggested to Fresnel that this and some further consequences should be tested experimentally; this was done, and the results were found to confirm the new theory. The concordance of observation and calculation was so admirable in all cases where a comparison was possible that the prize was awarded to Fresnel without further hesitation.
In the same year in which the memoir on diffraction was submitted, Fresnel published an investigation of the influence of the earth’s motion on light. We have already seen that aberration was explained by its discoverer in terms of the corpuscular theory; and it was Young who first showed how it may be explained on the wave-hypothesis.
“Upon considering the phenomena of the aberration of the stars,” he wrote, “I am disposed to believe that the luminiferous aether pervades the substance of all material bodies with little or no resistance, as freely perhaps as the wind passes through a grove of trees.”
In fact, if we suppose the aether surrounding the earth to be at rest and unaffected by the earth’s motion, the light-waves will not partake of the motion of the telescope, which we may suppose directed to the true place of the star. The image of the star will therefore be displaced from the central spider-line at the focus by a distance equal to that which the earth describes while the light is traveling through the telescope. This agrees with what is actually observed.
But a host of further questions now suggest themselves. Suppose, for instance, that a slab of glass with a plane face is moved along by the motion of the earth, and it is desired to adjust it so that a ray of light coming from a certain star shall not be bent when it enters the glass: must the surface be placed at right angles to the true direction of the star as freed from aberration, or to its apparent direction as affected by aberration?
The question of whether rays coming from the stars are refracted differently from rays originating in terrestrial sources had been raised originally by Michell; and Robison and Wilson had asserted that the focal length of an achromatic telescope should be increased when it is directed to a star toward which the earth is moving, owing to the change in the relative velocity of light.
Arago submitted the matter to the test of experiment and concluded that the light coming from any star behaves in all cases of reflection and refraction precisely as it would if the star were situated in the place which it appears to occupy in consequence of aberration, and the earth were at rest. So that the apparent refraction in a moving prism is equal to the absolute refraction in a fixed prism.
Fresnel now set out to provide a theory capable of explaining Arago’s result. To this end, he adopted Young’s suggestion, that the refractive powers of transparent bodies depend on the concentration of aether within them, and made it more precise by assuming that the aethereal density in any body is proportional to the square of the refractive index.
Thus, if [math]{ c }[/math] denote the velocity of light in vacuo, and if [math]{ c_1 }[/math] denote its velocity in a given material body at rest, so that
[math]{ \mu = \frac{c}{c_1} }[/math]
is the refractive index, then the densities [math]{ \rho }[/math] and [math]{ \rho_1 }[/math] of the aether in interplanetary space and in the body, respectively, will be connected by the relation
[math]{ \rho_1 = \mu^2 \rho }[/math]
Fresnel further assumed that, when a body is in motion, part of the aether within it is carried along—namely, that part which constitutes the excess of its density over the density of aether in vacuo; while the rest of the aether within the space occupied by the body is stationary.
Thus, the density of aether carried along is
[math]{ \rho_1 – \rho = (\mu^2 – 1) \rho }[/math],
while a quantity of aether of density [math]{ \rho }[/math] remains at rest.
The velocity with which the centre of gravity of the aether within the body moves forward in the direction of propagation is therefore
[math]{ \frac{(\mu^2 – 1) \rho}{\mu^2 \rho} w = \left( 1 – \frac{1}{\mu^2} \right) w }[/math],
where [math]{ w }[/math] denotes the component of the velocity of the body in this direction.
This is to be added to the velocity of propagation of the light-waves within the body; so that in the moving body the absolute velocity of light is
[math]{ c_1 + \left( 1 – \frac{1}{\mu^2} \right) w }[/math].
Many years afterwards, Stokes put the same supposition in a slightly different form. Suppose the whole of the aether within the body to move together, the aether entering the body in front, and being immediately condensed, and issuing from it behind, where it is immediately rarefied.
On this assumption, a mass [math]{ \rho w }[/math] of aether must pass in unit time across a plane of area unity, drawn anywhere within the body in a direction at right angles to the body’s motion.
Thus, the aether within the body has a drift-velocity
[math]{ – \frac{w \rho}{\rho_1} }[/math]
relative to the body.
So the velocity of light relative to the body will be
[math]{ c_1 – \frac{w \rho}{\rho_1} }[/math],
and the absolute velocity of light in the moving body will be
[math]{ c_1 + w – \frac{w \rho}{\rho_1} }[/math],
which simplifies to
[math]{ c_1 + \frac{w}{\mu^2} }[/math].
This formula was experimentally confirmed in 1851 by H. Fizeau, who measured the displacement of interference fringes formed by light that had passed through a column of moving water.
The same result may easily be deduced from an experiment performed by Hoek. In this experiment, a beam of light was divided into two portions, one of which was made to pass through a tube of water AB, was then reflected at a mirror C, and was afterwards allowed to return to A without passing through the water. The other portion of the bifurcated beam was made to describe the same path in the reverse order, i.e., passing through the water on its return journey from C instead of on the outward journey.
On causing the two portions of the beam to interfere, Hoek found that no difference of phase was produced between them when the apparatus was oriented in the direction of the terrestrial motion.
Let [math] w [/math] denote the velocity of the earth, supposed to be directed from the tube towards the mirror.
Let [math] \frac{c}{\mu} [/math] denote the velocity of light in the water at rest, and
[math] \frac{c}{\mu} + \varphi [/math]
the velocity of light in the water when moving.
Let [math] l [/math] denote the length of the tube. The magnitude of the distance BC does not affect the experiment, so we may suppose it zero.
The time taken by the first portion of the beam to perform its journey is evidently
[math] \frac{l}{\frac{c}{\mu} + \varphi – w} + \frac{l}{c + w} [/math]
where
[math] \varphi = \frac{(\mu^2 – 1) w}{\mu^2} [/math]
while the time for the second portion of the beam is
[math] \frac{l}{c – w} + \frac{l}{\frac{c}{\mu} – \varphi + w}. [/math]
The equality of these expressions gives at once, when terms of higher orders than the first in [math] \frac{w}{c} [/math] are neglected,
[math] \varphi = \frac{(\mu^2 – 1) w}{\mu^2}, [/math]
which is Fresnel’s expression.
On the basis of this formula, Fresnel proceeded to solve the problem of refraction in moving bodies.
Suppose that a prism A₀C₀B₀ is carried along by the earth’s motion in vacuo, its face A₀C₀ being at right angles to the direction of motion; and that light from a star is incident normally on this face. The rays experience no refraction at incidence, and we have only to consider the effect produced by the second surface A₀B₀.
Suppose that during an interval τ of time, the prism travels from the position A₀C₀B₀ to the position A₁C₁B₁, while the luminous disturbance at C₀ travels to B₁, and the luminous disturbance at A₀ travels to P, so that B₁P is the emergent wave-front.
Then we have
[math] C_0B_1 = \tau \left( c_1 + \frac{w}{\mu^2} \right) [/math],
[math] A_0D = \tau c, [/math]
[math] A_0A_1 = \tau w. [/math]
If we write [math] \angle C_1A_1B_1 = i [/math], and denote the total deviation of the wave-front by [math] \delta_1 [/math], we have
[math] A_1D = A_0D – A_1A_0 \cos \delta_1 = \tau c – \tau w \cos \delta_1. [/math]
Thus,
[math] \sin \angle A_1B_1D = \frac{c – w \cos \delta_1}{c_1} = \frac{c}{c_1} – \frac{w}{c_1} \cos \delta_1. [/math]
Denoting by [math] \delta [/math] the value of [math] \delta_1 [/math] when [math] w [/math] is zero, we have
[math] \frac{\sin (i – \delta)}{\sin i} = \frac{c}{c_1}. [/math]
Subtracting this equation from the preceding, we obtain
[math] \delta – \delta_1 = \frac{w}{c} \sin \delta. [/math]
Now the telescope by which the emergent wave-front B₁D is received is itself being carried forward by the earth’s motion; and we must therefore apply the usual correction for aberration in order to find the apparent direction of the emergent ray.
But this correction is
[math] \frac{w \sin \delta}{c}, [/math]
which precisely counteracts the effect calculated as due to the motion of the prism.
Thus, we finally see that the motion of the earth has no first-order influence on the refraction of light from the stars.
Fresnel inferred from his formula that if observations were made with a telescope filled with water, the aberration would be unaffected by the presence of the water—a result which was verified by Airy in 1871.
He showed, moreover, that:
- The apparent positions of terrestrial objects, carried along with the observer, are not displaced by the earth’s motion.
- Experiments in refraction and interference are not influenced by any motion that is common to the source, apparatus, and observer.
- Light travels between given points of a moving material system by the path of least time.
These predictions have also been confirmed by observation:
- Respighi (1861) and Hoek (1868), experimenting with a telescope filled with water and a terrestrial source of light, found that no effect was produced on the phenomena of reflection and refraction by altering the orientation of the apparatus relative to the direction of the earth’s motion.
- E. Mascart (1872) experimentally investigated the effect of the motion of the source or recipient of light, showing that the light of the sun and artificial sources alike are incapable of revealing the translatory motion of the earth through diffraction-phenomena.
The greatest problem now confronting the investigators of light was to reconcile the facts of polarization with the principles of the wave-theory.
Young had long been pondering over this but had hitherto been baffled. In 1816, he received a visit from Arago, who told him of a new experimental result, recently obtained by himself and Fresnel:
“Two pencils of light, polarized in planes at right angles, do not interfere with each other under circumstances in which ordinary light shows interference-phenomena, but always give by their reunion the same intensity of light, whatever be their difference of path.”
Arago had not long left him when Young, reflecting on the new experiment, discovered the long-sought key to the mystery:
The vibrations of light are executed at right angles to the direction of propagation.
This was precisely the alternative that Bernoulli had rejected eighty years before.
Young’s ideas were first embodied in a letter to Arago, dated January 12, 1817:
“I have been reflecting on the possibility of giving an imperfect explanation of the affection of light which constitutes polarization, without departing from the genuine doctrine of undulations. It is a principle in this theory that all undulations are simply propagated through homogeneous mediums in concentric spherical surfaces like the undulations of sound, consisting simply in the direct and retrograde motions of the particles in the direction of the radius, with their concomitant condensation and rarefactions. And yet it is possible to explain in this theory a transverse vibration, propagated also in the direction of the radius, and with equal velocity, the motions of the particles being in a certain constant direction with respect to that radius; and this is polarization.”
In an article on Chromatics, written in September 1817 for the supplement to the Encyclopaedia Britannica, he says:
“If we assume as a mathematical postulate, on the undulating theory, without attempting to demonstrate its physical foundation, that a transverse motion may be propagated in a direct line, we may derive from this assumption a tolerable illustration of the subdivision of polarized light by reflection in an oblique plane,” by “supposing the polar motion to be resolved” into two constituents, which fare differently at reflection.
In a further letter to Arago, dated April 29th, 1818, Young recurred to the subject of transverse vibrations, comparing light to the undulations of a cord agitated by one of its extremities.
This letter was shown by Arago to Fresnel, who at once saw that it presented the true explanation of the non-interference of beams polarized in perpendicular planes, and that the latter effect could even be made the basis of a proof of the correctness of Young’s hypothesis.
For if the vibration of each beam be supposed resolved into three components—one along the ray and the other two at right angles to it—it is obvious from the Arago-Fresnel experiment that the components in the direction of the ray must vanish.
In other words, the vibrations that constitute light are executed in the wave-front.
It must be remembered that the theory of the propagation of waves in an elastic solid was as yet unknown, and light was still always interpreted by analogy with the vibrations of sound in air, for which the direction of vibration is the same as that of propagation.
It was, therefore, necessary to give some justification for the new departure.
With wonderful insight, Fresnel indicated the precise direction in which the theory of vibrations in ponderable bodies needed to be extended in order to allow for waves similar to those of light:
“The geometers who have discussed the vibrations of elastic fluids hitherto have taken account of no accelerating forces except those arising from the difference of condensation or dilatation between consecutive layers.”
He pointed out that if we also suppose the medium to possess a rigidity, or power of resisting distortion, such as is manifested by all actual solid bodies, it will be capable of transverse vibration.
The absence of longitudinal waves in the aether he accounted for by supposing that the forces which oppose condensation are far more powerful than those which oppose distortion, and that the velocity with which condensations are propagated is so great compared with the speed of the oscillations of light, that a practical equilibrium of pressure is maintained perpetually.
The nature of ordinary non-polarized light was next discussed.
“If then,” Fresnel wrote, “the polarization of a ray of light consists in this, that all its vibrations are executed in the same direction, it results from any hypothesis on the generation of light-waves, that a ray emanating from a single centre of disturbance will always be polarized in a definite plane at any instant.
But an instant afterwards, the direction of the motion changes, and with it the plane of polarization; and these variations follow each other as quickly as the perturbations of the vibrations of the luminous particle: so that even if we could isolate the light of this particular particle from that of other luminous particles, we should doubtless not recognize in it any appearance of polarization.
If we consider now the effect produced by the union of all the waves which emanate from the different points of a luminous body, we see that at each instant, at a definite point of the aether, the general resultant of all the motions which commingle there will have a determinate direction, but this direction will vary from one instant to the next.
So direct light can be considered as the union, or more exactly as the rapid succession, of systems of waves polarized in all directions.
According to this way of looking at the matter, the act of polarization consists not in creating these transverse motions, but in decomposing them into two invariable directions, and separating the components from each other; for then, in each of them, the oscillatory motions take place always in the same plane.”
He then proceeded to consider the relation of the direction of vibration to the plane of polarization.
“Apply these ideas to double refraction, and regard a uniaxial crystal as an elastic medium in which the accelerating force that results from the displacement of a row of molecules perpendicular to the axis, relative to contiguous rows, is the same all around the axis; while the displacements parallel to the axis produce accelerating forces of a different intensity—stronger if the crystal is “repulsive” and weaker if it is “attractive.”
The distinctive character of the rays that are ordinarily refracted is that they propagate themselves with the same velocity in all directions.
We must admit that their oscillatory motions are executed at right angles to the plane drawn through these rays and the axis of the crystal; for then, the displacements that they occasion, always taking place along directions perpendicular to the axis, will, by hypothesis, always give rise to the same accelerating forces.
But, with the conventional meaning attached to the expression plane of polarization, the plane of polarization of the ordinary rays is the plane through the axis.
Thus, in a pencil of polarized light, the oscillatory motion is executed at right angles to the plane of polarization.”
This result afforded Fresnel a foothold in dealing with the problem that occupied the rest of his life: henceforth, his aim was to base the theory of light on the dynamical properties of the luminiferous medium.
The first topic that he attacked from this point of view was the propagation of light in crystalline bodies.
Since Brewster’s discovery that many crystals do not conform to the type to which Huygens’ construction is applicable, the wave theory had to some extent lost credit in this region.
Fresnel, now, by what was perhaps the most brilliant of all his efforts, not only reconquered the lost territory, but also added a new domain to science.
He had, as he tells us himself, never believed the doctrine that in crystals there are two different luminiferous media, one to transmit the ordinary waves, and the other to transmit the extraordinary waves.
The alternative to which he inclined was that the two velocities of propagation were really the two roots of a quadratic equation, derivable in some way from the theory of a single aether.
Could this equation be obtained, he was confident of finding the explanation, not only of double refraction, but also of the polarization by which it is always accompanied.
The first step was to take the case of uniaxial crystals, which had been discussed by Huygens, and to see whether Huygens’ sphere and spheroid could be replaced by, or made to depend on, a single surface.
Now, a wave propagated in any direction through a uniaxial crystal can be resolved into two plane-polarized components. One of these, the ordinary ray, is polarized in the principal section and has a velocity [math] v_1 [/math], which may be represented by the radius of Huygens’ sphere—say,
[math] v_1 = \frac{c}{\mu} [/math],
while the other, the extraordinary ray, is polarized in a plane at right angles to the principal section and has a wave-velocity [math] v_2 [/math], which may be represented by the perpendicular drawn from the centre of Huygens’ spheroid on the tangent-plane parallel to the plane of the wave.
If the spheroid be represented by the equation
[math] \frac{y^2 + z^2}{b^2} + \frac{x^2}{a^2} = 1, [/math]
and if (l, m, n) denote the direction-cosines of the normal to the plane of the wave, we have, therefore,
[math] v_2^2 = a^2 (m^2 + n^2) + b^2 l^2. [/math]
But the quantities [math] 1/v_1 [/math] and [math] 1/v_2 [/math], as given by these equations, are easily seen to be the lengths of the semi-axes of the ellipse in which the spheroid
[math] \frac{y^2 + z^2}{b^2} + \frac{x^2}{a^2} = 1 [/math]
is intersected by the plane
[math] l x + m y + n z = 0. [/math]
Thus, the construction in terms of Huygens’ sphere and spheroid can be replaced by one which depends only on a single surface, namely the spheroid
[math] \frac{y^2 + z^2}{b^2} + \frac{x^2}{a^2} = 1. [/math]
Having achieved this reduction, Fresnel guessed that the case of biaxial crystals could be covered by substituting for the latter spheroid an ellipsoid with three unequal axes—say,
[math] \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1. [/math]
If [math] 1/v_1 [/math] and [math] 1/v_2 [/math] denote the lengths of the semi-axes of the ellipse in which this ellipsoid is intersected by the plane
[math] l x + m y + n z = 0, [/math]
it is well known that [math] v_1 [/math] and [math] v_2 [/math] are the roots of the equation in [math] v_2 [/math]:
[math] \frac{l^2}{v_2^2 – a^2} + \frac{m^2}{v_2^2 – b^2} + \frac{n^2}{v_2^2 – c^2} = 0. [/math]
Accordingly, Fresnel conjectured that the roots of this equation represent the velocities, in a biaxial crystal, of the two plane-polarized waves whose normals are in the direction [math] (l, m, n) [/math].
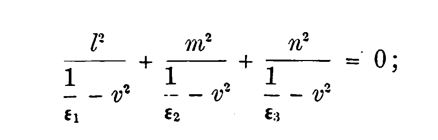
Having thus arrived at his result by reasoning of a purely geometrical character, he now devised a dynamical scheme to suit it.
The vibrating medium within a crystal he supposed to be ultimately constituted of particles subjected to mutual forces; and on this assumption, he showed that the elastic force of restitution, when the system is disturbed, must depend linearly on the displacement.
In this first proposition, a difference is apparent between Fresnel’s theory and a true elastic-solid theory; for in actual elastic solids, the forces of restitution depend not on the absolute displacement, but on the strains, i.e., the relative displacements.
In any crystal, there will exist three directions at right angles to each other, for which the force of restitution acts in the same line as the displacement. These directions are named axes of elasticity.
Let these be taken as coordinate axes, and suppose that the elastic forces of restitution for unit displacements in these three directions are [math] \frac{1}{\varepsilon_1} [/math], [math] \frac{1}{\varepsilon_2} [/math], and [math] \frac{1}{\varepsilon_3} [/math], respectively.
That the elasticity should vary with the direction of the molecular displacement seemed to Fresnel to suggest that the molecules of the material body either take part in the luminous vibration, or at any rate influence in some way the elasticity of the aether.
A unit displacement in any arbitrary direction [math] (\alpha, \beta, \gamma) [/math] can be resolved into component displacements [math] (\cos \alpha, \cos \beta, \cos \gamma) [/math] parallel to the axes, and each of these produces its own effect independently.
So the components of the force of restitution are
[math]
\frac{\cos^2 \alpha}{\varepsilon_1}, \quad
\frac{\cos^2 \beta}{\varepsilon_2}, \quad
\frac{\cos^2 \gamma}{\varepsilon_3}.
[/math]
This resultant force does not in general have the same direction as the displacement that produced it; but it may always be decomposed into two other forces—one parallel and the other perpendicular to the direction of the displacement.
The former of these is evidently
[math]
\frac{\cos^2 \alpha}{\varepsilon_1} +
\frac{\cos^2 \beta}{\varepsilon_2} +
\frac{\cos^2 \gamma}{\varepsilon_3}.
[/math]
The surface
[math]
\frac{x^2}{\varepsilon_1} +
\frac{y^2}{\varepsilon_2} +
\frac{z^2}{\varepsilon_3} = 1
[/math]
will therefore have the property that the square of its radius vector in any direction is proportional to the component in that direction of the elastic force due to a unit displacement in that direction.
This surface is called the surface of elasticity.
Consider now a displacement along one of the axes of the section on which the surface of elasticity is intersected by the plane of the wave.
It is easily seen that, in this case, the component of the elastic force at right angles to the displacement acts along the normal to the wave-front.
Fresnel assumes that it will be without influence on the propagation of the vibrations, on the ground of his fundamental hypothesis that the vibrations of light are performed solely in the wave-front.
This step is evidently open to criticism; for in a dynamical theory, everything should be deduced from the laws of motion without special assumptions.
But granting his contention, it follows that such a displacement will retain its direction, and will be propagated as a plane-polarized wave with a definite velocity.
Now, in order that a stretched cord may vibrate with unchanged period, when its tension is varied, its length must be increased proportionally to the square root of its tension.
Similarly, the wavelength of a luminous vibration of given period is proportional to the square root of the elastic force (per unit displacement), which urges the molecules of the medium parallel to the wave-front.
Hence, the velocity of propagation of a wave, measured at right angles to its front, is proportional to the square root of the component, along the direction of displacement, of the elastic force per unit displacement.
Thus, the velocity of propagation of such a plane-polarized wave as we have considered is proportional to the radius vector of the surface of elasticity in the direction of displacement.
Moreover, any displacement in the given wave-front can be resolved into two, which are respectively parallel to the two axes of the diametral section of the surface of elasticity by a plane parallel to this wave-front.
It follows from what has been said that each of these component displacements will be propagated as an independent plane-polarized wave, the velocities of propagation being proportional to the axes of the section, and therefore inversely proportional to the axes of the section of the inverse surface of this with respect to the origin, which is the ellipsoid
[math]
\frac{x^2}{\varepsilon_1} + \frac{y^2}{\varepsilon_2} + \frac{z^2}{\varepsilon_3} = 1.
[/math]
But this is precisely the result to which, as we have seen, Fresnel had been led by purely geometrical considerations; and thus his geometrical conjecture could now be regarded as substantiated by a study of the dynamics of the medium.
It is easy to determine the wave-surface, or locus at any instant—say, [math] t = 1 [/math]—of a disturbance originated at some previous instant—say, [math] t = 0 [/math]—at some particular point—say, the origin.
For this wave-surface will evidently be the envelope of plane waves emitted from the origin at the instant [math] t = 0 [/math]—that is, it will be the envelope of planes
[math]
l x + m y + n z – v = 0,
[/math]
where the constants [math] l, m, n, v [/math] are connected by the identical equation
[math]
l^2 + m^2 + n^2 = 1,
[/math]
and by the relation previously found—namely,
[math]
\frac{l^2}{\varepsilon_1} + \frac{m^2}{\varepsilon_2} + \frac{n^2}{\varepsilon_3} = \frac{1}{v^2}.
[/math]
By the usual procedure for determining envelopes, it may be shown that the locus in question is the surface of the fourth degree
[math]
\frac{x^2}{\varepsilon_1} + \frac{y^2}{\varepsilon_2} + \frac{z^2}{\varepsilon_3} +
\frac{x^2}{\varepsilon_2 – \varepsilon_1} + \frac{y^2}{\varepsilon_3 – \varepsilon_2} + \frac{z^2}{\varepsilon_1 – \varepsilon_3} = 0,
[/math]
which is called Fresnel’s wave-surface.
It is a two-sheeted surface, as must evidently be the case from physical considerations.
In uniaxial crystals, for which [math] \varepsilon_2 [/math] and [math] \varepsilon_3 [/math] are equal, it degenerates into the sphere
[math]
v = \sqrt{\varepsilon_2},
[/math]
and the spheroid
[math]
\varepsilon_2 x^2 + \varepsilon_1 (y^2 + z^2) = 1.
[/math]
It is to these two surfaces that tangent-planes are drawn in the construction given by Huygens for the ordinary and extraordinary refracted rays in Iceland spar.
As Fresnel observed, exactly the same construction applies to biaxial crystals, when the two sheets of the wave-surface are substituted for Huygens’ sphere and spheroid.
“The theory which I have adopted,” says Fresnel at the end of this memorable paper, “and the simple constructions which I have deduced from it, have this remarkable character, that all the unknown quantities are determined together by the solution of the problem. We find at the same time the velocities of the ordinary ray and of the extraordinary ray, and their planes of polarization. Physicists who have studied attentively the laws of nature will feel that such simplicity and such close relations between the different elements of the phenomenon are conclusive in favour of the hypothesis on which they are based.”
The question as to the correctness of Fresnel’s construction was discussed for many years afterwards.
A striking consequence of it was pointed out in 1832 by William Rowan Hamilton (b. 1805, d. 1865), Royal Astronomer of Ireland, who remarked that the surface defined by Fresnel’s equation has four conical points, at each of which there is an infinite number of tangent planes.
Consequently, a single ray, proceeding from a point within the crystal in the direction of one of these points, must be divided on emergence into an infinite number of rays, constituting a conical surface.
Hamilton also showed that there are four planes, each of which touches the wave-surface in an infinite number of points, constituting a circle of contact.
Thus, a corresponding ray incident externally should be divided within the crystal into an infinite number of refracted rays, again constituting a conical surface.
These singular and unexpected consequences of the theory were shortly afterwards verified experimentally by Humphrey Lloyd, and helped greatly to confirm belief in Fresnel’s theory.
It should, however, be observed that conical refraction only shows his form of the wave-surface to be correct in its general features, and is no test of its accuracy in all details.
But it was shown experimentally by Stokes in 1872, Glazebrook in 1879, and Hastings in 1887, that the construction of Huygens and Fresnel is certainly correct to a very high degree of approximation; and Fresnel’s final formulae have since been regarded as unassailable.
The dynamical substructure on which he based them is, as we have seen, open to objection; but, as Stokes observed:
“If we reflect on the state of the subject as Fresnel found it, and as he left it, the wonder is, not that he failed to give a rigorous dynamical theory, but that a single mind was capable of effecting so much.”
As in his previous investigations, he assumes that the vibrations which constitute light are executed at right angles to the plane of polarization. He adopts Young’s principle, that reflexion and refraction are due to differences in the inertia of the aether in different material bodies, and supposes (as in his memoir on Aberration) that the inertia is proportional to the inverse square of the velocity of propagation of light in the medium. The conditions which he proposes to satisfy at the interface between two media, are that the displacements of the adjacent molecules, resolved parallel to this interface, shall be equal in the two media; and that the energy of the reflected and refracted waves together shall be equal to that of the incident wave.
On these assumptions the intensity of the reflected and refracted light may be obtained in the following way:—
Consider first the case in which the incident light is polarized in the plane of incidence, so that the displacement is at right angles to the plane of incidence; let the amplitude of the displacement at a given point of the interface be [math] f [/math] for the incident ray, [math] g [/math] for the reflected ray, and [math] h [/math] for the refracted ray.
The quantities of energy propagated per second across unit cross-section of the incident, reflected, and refracted beams are proportional respectively to
[math]
\frac{c_1 \rho_1 f^2}{\cos i}, \quad
\frac{c_1 \rho_1 g^2}{\cos i}, \quad
\frac{c_2 \rho_2 h^2}{\cos r}.
[/math]The principle of conservation of energy therefore gives
[math]
c_1 \rho_1 \cos i \cdot f^2 = c_1 \rho_1 \cos i \cdot g^2 + c_2 \rho_2 \cos r \cdot h^2.
[/math]The equation of continuity of displacement at the interface is
[math]
f + g = h,
[/math]where [math] c_1, c_2 [/math] denote the velocities of light, and [math] \rho_1, \rho_2 [/math] the densities of aether, in the two media; and the cross-sections of the beams which meet the interface in unit area are given respectively.

Eliminating [math] h [/math] between these two equations, and using the formula
[math]
\frac{\sin^2 r}{\sin^2 i} = \frac{c_2^2 \rho_1}{c_1^2 \rho_2},
[/math]
we obtain the equation
[math]
\frac{g}{f} = \frac{\sin (i – r)}{\sin (i + r)}.
[/math]
Thus, when the light is polarized in the plane of reflexion, the amplitude of the reflected wave is
[math]
\frac{\sin (i – r)}{\sin (i + r)} \times
\text{(the amplitude of the incident vibration)}.
[/math]
Fresnel shows in a similar way that when the light is polarized at right angles to the plane of reflexion, the ratio of the amplitudes of the reflected and incident waves is
[math]
\frac{\tan (i – r)}{\tan (i + r)}.
[/math]
These formulae are generally known as Fresnel’s sine-law and Fresnel’s tangent-law respectively. They had, however, been discovered experimentally by Brewster some years previously.
When the incidence is perpendicular, so that [math] i [/math] and [math] r [/math] are very small, the ratio of the amplitudes becomes
[math]
\lim_{i, r \to 0} \frac{i – r}{i + r},
[/math]
or
[math]
\frac{\mu_2 – \mu_1}{\mu_2 + \mu_1},
[/math]
where [math] \mu_2 [/math] and [math] \mu_1 [/math] denote the refractive indices of the media.
This formula had been given previously by Young and Poisson, on the supposition that the elasticity of the aether is of the same kind as that of air in sound.
When i f r = 90o, tan (i + r) becomes infinite : and thus a theoretical explanation is obtained for Brewster,s law, that if the incidence is such as to make the reflected and refracted rays.
When [math] i + r = 90^\circ [/math], [math] \tan (i + r) [/math] becomes infinite: and thus a theoretical explanation is obtained for Brewster’s law, that if the incidence is such as to make the reflected and refracted rays perpendicular to each other, the reflected light will be wholly polarized in the plane of reflexion.
Fresnel’s investigation can scarcely be called a dynamical theory in the strict sense, as the qualities of the medium are not defined. His method was to work backwards from the known properties of light, in the hope of arriving at a mechanism to which they could be attributed; he succeeded in accounting for the phenomena in terms of a few simple principles, but was not able to specify an aether which would in turn account for these principles.
The “displacement” of Fresnel could not be a displacement in an elastic solid of the usual type, since its normal component is not continuous across the interface between two media.
The theory of ordinary reflexion was completed by a discussion of the case in which light is reflected totally.
This had formed the subject of some of Fresnel’s experimental researches several years before; and in two papers presented to the Academy in November, 1817, and January, 1818, he had shown that light polarized in any plane inclined to the plane of reflexion is partly “depolarized” by total reflexion, and that this is due to differences of phase which are introduced between the components polarized in and perpendicular to the plane of reflexion.
“When the reflexion is total,” he said, “rays polarized in the plane of reflexion are reflected nearer the surface of the glass than those polarized at right angles to the same plane, so that there is a difference in the paths described.”
This change of phase he now deduced from the formulae already obtained for ordinary reflexion.
Considering light polarized in the plane of reflexion, the ratio of the amplitudes of the reflected and incident light is, as we have seen,
[math]
\frac{\sin (i – r)}{\sin (i + r)}.
[/math]
When the sine of the angle of incidence is greater than [math] \mu_2 / \mu_1 [/math], so that total reflexion takes place, this ratio may be written in the form
[math]
e^{\theta \sqrt{-1}},
[/math]
where [math] \theta [/math] denotes a real quantity defined by the equation
[math]
\tan \theta = \frac{\left( \mu_1^2 \sin^2 i – \mu_2^2 \right)^{\frac{1}{2}}}{\mu_1 \cos i}.
[/math]
Fresnel interpreted this expression to mean that the amplitude of the reflected light is equal to that of the incident, but that the two waves differ in phase by an amount [math] \theta [/math].
The case of light polarized at right angles to the plane of reflexion may be treated in the same way, and the resulting formulae are completely confirmed by experiment.
A few months after the memoir on reflexion had been presented, Fresnel was elected to a seat in the Academy; and during the rest of his short life, honours came to him both from France and abroad.
In 1827, the Royal Society awarded him the Rumford medal; but Arago, to whom Young had confided the mission of conveying the medal, found him dying; and eight days afterwards, he breathed his last.
By the genius of Young and Fresnel, the wave-theory of light was established in a position which has since remained unquestioned; and it seemed almost a work of supererogation when, in 1850, Foucault and Fizeau, carrying out a plan long before imagined by Arago, directly measured the velocity of light in air and in water, and found that on the question so long debated between the rival schools, the adherents of the undulatory theory had been in the right.