WildTrig playlist – https://youtube.com/playlist?list=PLIljB45xT85CyF_7bKd6y36VArOy3p2oh&si=yN_j1mo9EysTcfoq
1 Why Trig is Hard | WildTrig: Intro to Rational Trigonometry | N J Wildberger
00:00 Introduction to the series on rational trig 01:00 Trigonometry and triangle measurements 03:14 Distance and angle: are they really fundamental? 06:13 The classical sine function and intrinsic irrationalities
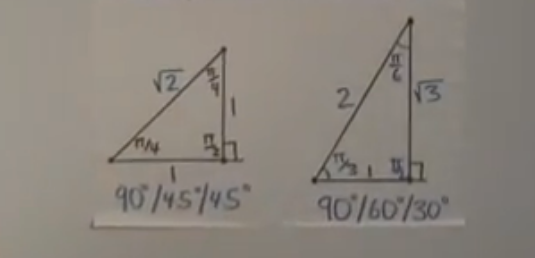
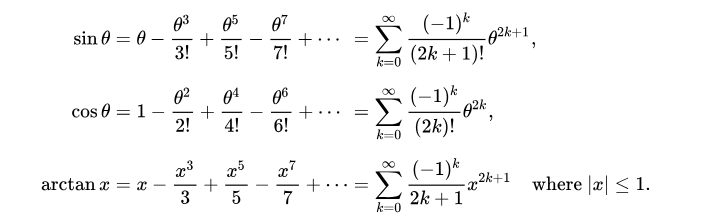
2.
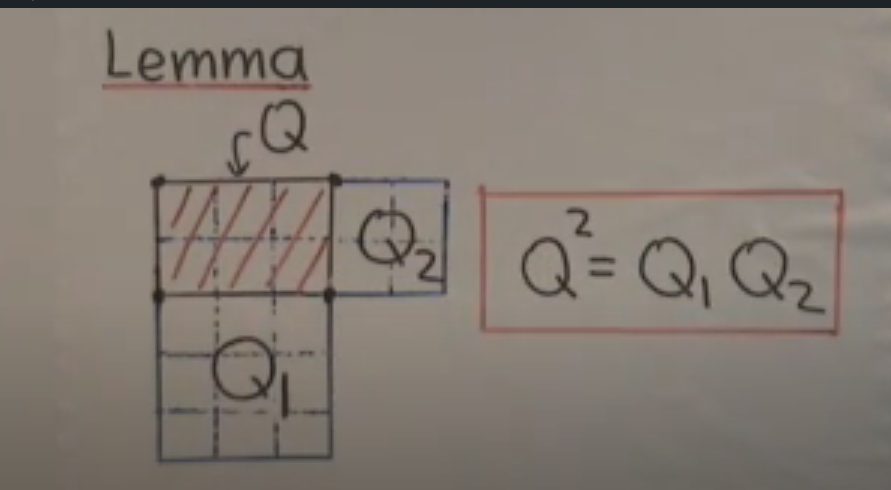


3.
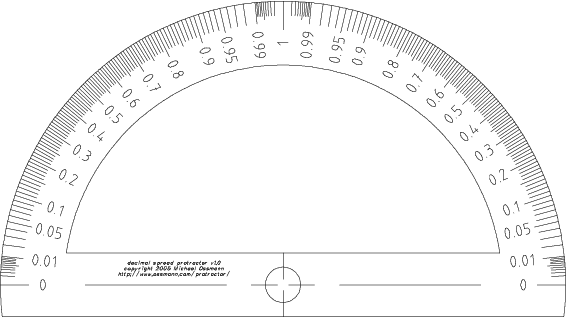
source: https://www.researchgate.net/figure/A-spread-protractor_fig4_284572258
4. Five Main Laws of Rational Trigonometry | WildTrig: Intro to Rational Trigonometry | N J Wildberger
27. Stewart’s theorem | WildTrig: N J Wildberger
Trigonometric identities play a crucial role in simplifying equations in mathematics, physics, and engineering. Below is a list of fundamental trigonometric identities, carefully formatted to work on your website.
Find in page how Pythagorean Identities are used here:
1. Pythagorean Identities
- [math] \sin^2 x + \cos^2 x = 1 [/math]
- [math] 1 + \tan^2 x = \sec^2 x [/math]
- [math] 1 + \cot^2 x = \csc^2 x [/math]
2. Reciprocal Identities
- [math] \sin x = \frac{1}{\csc x} [/math], [math] \csc x = \frac{1}{\sin x} [/math]
- [math] \cos x = \frac{1}{\sec x} [/math], [math] \sec x = \frac{1}{\cos x} [/math]
- [math] \tan x = \frac{1}{\cot x} [/math], [math] \cot x = \frac{1}{\tan x} [/math]
3. Quotient Identities
- [math] \tan x = \frac{\sin x}{\cos x} [/math]
- [math] \cot x = \frac{\cos x}{\sin x} [/math]
4. Co-Function Identities
- [math] \sin(90^\circ – x) = \cos x [/math], [math] \cos(90^\circ – x) = \sin x [/math]
- [math] \tan(90^\circ – x) = \cot x [/math], [math] \cot(90^\circ – x) = \tan x [/math]
- [math] \sec(90^\circ – x) = \csc x [/math], [math] \csc(90^\circ – x) = \sec x [/math]
5. Even-Odd Identities
- [math] \sin(-x) = -\sin x [/math]
- [math] \cos(-x) = \cos x [/math]
- [math] \tan(-x) = -\tan x [/math]
- [math] \cot(-x) = -\cot x [/math]
- [math] \sec(-x) = \sec x [/math]
- [math] \csc(-x) = -\csc x [/math]
6. Sum and Difference Formulas
- [math] \sin(A \pm B) = \sin A \cos B \pm \cos A \sin B [/math]
- [math] \cos(A \pm B) = \cos A \cos B \mp \sin A \sin B [/math]
- [math] \tan(A \pm B) = \frac{\tan A \pm \tan B}{1 \mp \tan A \tan B} [/math]
7. Double-Angle Identities
- [math] \sin 2x = 2 \sin x \cos x [/math]
- [math] \cos 2x = \cos^2 x – \sin^2 x [/math]
- Alternative forms:
- [math] \cos 2x = 2 \cos^2 x – 1 [/math]
- [math] \cos 2x = 1 – 2 \sin^2 x [/math]
- [math] \tan 2x = \frac{2 \tan x}{1 – \tan^2 x} [/math]
8. Half-Angle Identities
- [math] \sin \frac{x}{2} = \pm \sqrt{\frac{1 – \cos x}{2}} [/math]
- [math] \cos \frac{x}{2} = \pm \sqrt{\frac{1 + \cos x}{2}} [/math]
- [math] \tan \frac{x}{2} = \pm \sqrt{\frac{1 – \cos x}{1 + \cos x}} [/math]
- Alternative forms:
- [math] \tan \frac{x}{2} = \frac{\sin x}{1 + \cos x} [/math]
- [math] \tan \frac{x}{2} = \frac{1 – \cos x}{\sin x} [/math]
9. Product-to-Sum Identities
- [math] \sin A \sin B = \frac{1}{2} [\cos(A – B) – \cos(A + B)] [/math]
- [math] \cos A \cos B = \frac{1}{2} [\cos(A – B) + \cos(A + B)] [/math]
- [math] \sin A \cos B = \frac{1}{2} [\sin(A + B) + \sin(A – B)] [/math]
10. Sum-to-Product Identities
- [math] \sin A + \sin B = 2 \sin \frac{A + B}{2} \cos \frac{A – B}{2} [/math]
- [math] \sin A – \sin B = 2 \cos \frac{A + B}{2} \sin \frac{A – B}{2} [/math]
- [math] \cos A + \cos B = 2 \cos \frac{A + B}{2} \cos \frac{A – B}{2} [/math]
- [math] \cos A – \cos B = -2 \sin \frac{A + B}{2} \sin \frac{A – B}{2} [/math]
11. Special Trigonometric Identities for AC Circuits
These identities are particularly useful in Peak and RMS Voltage calculations.
- [math] \cos^2 x = \frac{1 + \cos 2x}{2} [/math]
- [math] \sin^2 x = \frac{1 – \cos 2x}{2} [/math]
3. Quotient Identities
Mathematics is full of elegant identities that simplify complex problems. One of the most useful identities in electrical engineering appears when calculating instantaneous power in AC circuits. This identity is:
[math] \cos^2 x = \frac{1 + \cos 2x}{2} [/math]
This trigonometric property naturally emerges when dealing with Peak and RMS Voltage, helping us understand how power oscillates in an AC circuit.
Peak and RMS Voltage Calculation Using Trigonometric Identities
In an AC circuit with a purely resistive load, the voltage and current follow sinusoidal waveforms:
[math] v(t) = V_{\text{peak}} \cos(\omega t) [/math]
[math] i(t) = I_{\text{peak}} \cos(\omega t) [/math]
The instantaneous power is given by:
[math] P(t) = v(t) \cdot i(t) [/math]
Substituting the voltage and current expressions:
[math] P(t) = V_{\text{peak}} \cos(\omega t) \cdot I_{\text{peak}} \cos(\omega t) [/math]
Using the trigonometric identity:
[math] \cos^2 x = \frac{1 + \cos(2x)}{2} [/math]
we can rewrite the power equation as:
[math] P(t) = V_{\text{peak}} I_{\text{peak}} \frac{1 + \cos(2\omega t)}{2} [/math]
or:
[math] P(t) = \frac{V_{\text{peak}} I_{\text{peak}}}{2} (1 + \cos(2\omega t)) [/math]
This shows that the power oscillates at twice the frequency of the original voltage and current waveforms.
Converting to RMS Voltage
The RMS (Root Mean Square) voltage is related to the peak voltage by:
[math] V_{\text{rms}} = \frac{V_{\text{peak}}}{\sqrt{2}} [/math]
Squaring both sides:
[math] V_{\text{rms}}^2 = \frac{V_{\text{peak}}^2}{2} [/math]
This allows us to rewrite the power equation in terms of RMS voltage:
[math] P(t) = \frac{V_{\text{rms}}^2}{R} (1 + \cos(2\omega t)) [/math]
Here, the factor of 12\frac{1}{2}21 disappears, because it has already been incorporated into the RMS definition.
Conclusion
The trigonometric identity:
[math] \cos^2 x = \frac{1 + \cos 2x}{2} [/math]
naturally appears in AC power calculations, simplifying the expression for instantaneous power and justifying the use of RMS values in electrical engineering.
Math Tips and Tricks: Trigonometric Identities - When They Appear
In electrical engineering, particularly when dealing with alternating current (AC) signals, we frequently encounter the need to calculate peak and root-mean-square (RMS) voltages. These calculations often involve trigonometric identities, specifically those related to the cosine function. Let's delve into how the identity leading to (1 + cos(2ωt)) arises and its significance.
Understanding the Foundation
Consider a sinusoidal AC voltage signal, represented by:[math]v(t) = V_p \cos(\omega t)[/math]
where: * v(t) is the instantaneous voltage at time t. * Vp is the peak voltage. * ω is the angular frequency. To calculate the RMS voltage, we need to find the square root of the mean of the squared voltage over one period. This involves squaring the voltage signal:
[math]v^2(t) = (V_p \cos(\omega t))^2 = V_p^2 \cos^2(\omega t)[/math]
Here’s where the trigonometric identity comes into play. We need to express cos²(ωt) in a form that’s easier to integrate over a period. We use the double-angle identity:
[math]\cos(2\theta) = 2\cos^2(\theta) – 1[/math]
Rearranging this identity to solve for cos²(θ), we get:
[math]\cos^2(\theta) = \frac{1 + \cos(2\theta)}{2}[/math]
Substituting ωt for θ, we have:
[math]\cos^2(\omega t) = \frac{1 + \cos(2\omega t)}{2}[/math]
Therefore, the squared voltage becomes:
[math]v^2(t) = V_p^2 \left(\frac{1 + \cos(2\omega t)}{2}\right)[/math]
RMS Voltage Calculation The RMS voltage (Vrms) is calculated as:
[math]V_{rms} = \sqrt{\frac{1}{T} \int_0^T v^2(t) dt}[/math]
where T is the period of the signal. Substituting the expression for v²(t):
[math]V_{rms} = \sqrt{\frac{1}{T} \int_0^T V_p^2 \left(\frac{1 + \cos(2\omega t)}{2}\right) dt}[/math]
[math]V_{rms} = V_p \sqrt{\frac{1}{2T} \int_0^T (1 + \cos(2\omega t)) dt}[/math] The integral of cos(2ωt) over one period is zero, leaving:
[math]V_{rms} = V_p \sqrt{\frac{1}{2T} \int_0^T 1 dt} = V_p \sqrt{\frac{1}{2T} \cdot T} = \frac{V_p}{\sqrt{2}}[/math]
Significance of the Identity The trigonometric identity cos²(ωt) = (1 + cos(2ωt))/2 is crucial because it transforms a squared trigonometric function into a form that’s easily integrated. This allows us to derive the relationship between peak and RMS voltages, which is fundamental in AC circuit analysis. In summary, the appearance of the term (1 + cos(2ωt)) stems directly from the double-angle identity for cosine, facilitating the calculation of RMS voltage from peak voltage.